Added value of PCR testing for COVID-19
During the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) pandemic, polymerase chain reaction (PCR) tests were generally reported only as binary positive or negative outcomes. However, these test results contain a great deal more information than that. As viral load declines exponentially, the PCR cycle threshold (Ct) increases linearly. Hay et al. developed an approach for extracting epidemiological information out of the Ct values obtained from PCR tests used in surveillance for a variety of settings (see the Perspective by Lopman and McQuade). Although there are challenges to relying on single Ct values for individual-level decision-making, even a limited aggregation of data from a population can inform on the trajectory of the pandemic. Therefore, across a population, an increase in aggregated Ct values indicates that a decline in cases is occurring.
Science, abh0635, this issue p. eabh0635; see also abj4185, p. 280
Structured Abstract
INTRODUCTION
Current approaches to epidemic monitoring rely on case counts, test positivity rates, and reported deaths or hospitalizations. These metrics, however, provide a limited and often biased picture as a result of testing constraints, unrepresentative sampling, and reporting delays. Random cross-sectional virologic surveys can overcome some of these biases by providing snapshots of infection prevalence but currently offer little information on the epidemic trajectory without sampling across multiple time points.
RATIONALE
We develop a new method that uses information inherent in cycle threshold (Ct) values from reverse transcription quantitative polymerase chain reaction (RT-qPCR) tests to robustly estimate the epidemic trajectory from multiple or even a single cross section of positive samples. Ct values are related to viral loads, which depend on the time since infection; Ct values are generally lower when the time between infection and sample collection is short. Despite variation across individuals, samples, and testing platforms, Ct values provide a probabilistic measure of time since infection. We find that the distribution of Ct values across positive specimens at a single time point reflects the epidemic trajectory: A growing epidemic will necessarily have a high proportion of recently infected individuals with high viral loads, whereas a declining epidemic will have more individuals with older infections and thus lower viral loads. Because of these changing proportions, the epidemic trajectory or growth rate should be inferable from the distribution of Ct values collected in a single cross section, and multiple successive cross sections should enable identification of the longer-term incidence curve. Moreover, understanding the relationship between sample viral loads and epidemic dynamics provides additional insights into why viral loads from surveillance testing may appear higher for emerging viruses or variants and lower for outbreaks that are slowing, even absent changes in individual-level viral kinetics.
RESULTS
Using a mathematical model for population-level viral load distributions calibrated to known features of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) viral load kinetics, we show that the median and skewness of Ct values in a random sample change over the course of an epidemic. By formalizing this relationship, we demonstrate that Ct values from a single random cross section of virologic testing can estimate the time-varying reproductive number of the virus in a population, which we validate using data collected from comprehensive SARS-CoV-2 testing in long-term care facilities. Using a more flexible approach to modeling infection incidence, we also develop a method that can reliably estimate the epidemic trajectory in even more-complex populations, where interventions may be implemented and relaxed over time. This method performed well in estimating the epidemic trajectory in the state of Massachusetts using routine hospital admissions RT-qPCR testing data—accurately replicating estimates from other sources for the entire state.
CONCLUSION
This work provides a new method for estimating the epidemic growth rate and a framework for robust epidemic monitoring using RT-qPCR Ct values that are often simply discarded. By deploying single or repeated (but small) random surveillance samples and making the best use of the semiquantitative testing data, we can estimate epidemic trajectories in real time and avoid biases arising from nonrandom samples or changes in testing practices over time. Understanding the relationship between population-level viral loads and the state of an epidemic reveals important implications and opportunities for interpreting virologic surveillance data. It also highlights the need for such surveillance, as these results show how to use it most informatively.
(A and B) Whether an epidemic has rising or falling incidence will be reflected in the distribution of times since infection (A), which in turn affects the distribution of Ct values in a surveillance sample (B). (C) These values can be used to assess whether the epidemic is rising or falling and estimate the incidence curve.
” data-icon-position=”” data-hide-link-title=”0″>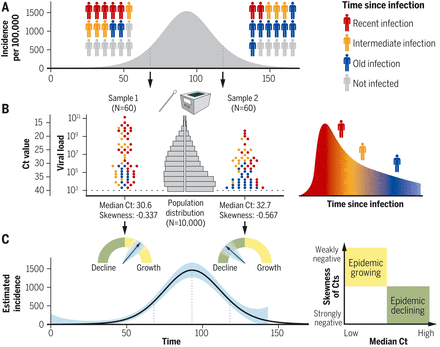

(A and B) Whether an epidemic has rising or falling incidence will be reflected in the distribution of times since infection (A), which in turn affects the distribution of Ct values in a surveillance sample (B). (C) These values can be used to assess whether the epidemic is rising or falling and estimate the incidence curve.
Abstract
Estimating an epidemic’s trajectory is crucial for developing public health responses to infectious diseases, but case data used for such estimation are confounded by variable testing practices. We show that the population distribution of viral loads observed under random or symptom-based surveillance—in the form of cycle threshold (Ct) values obtained from reverse transcription quantitative polymerase chain reaction testing—changes during an epidemic. Thus, Ct values from even limited numbers of random samples can provide improved estimates of an epidemic’s trajectory. Combining data from multiple such samples improves the precision and robustness of this estimation. We apply our methods to Ct values from surveillance conducted during the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) pandemic in a variety of settings and offer alternative approaches for real-time estimates of epidemic trajectories for outbreak management and response.
Real-time tracking of the epidemic trajectory and infection incidence is fundamental for public health planning and intervention during a pandemic (1, 2). In the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) pandemic, key epidemiological parameters, such as the effective reproductive number Rt, have typically been estimated using the time series of observed case counts, hospitalizations, or deaths, usually on the basis of reverse transcription quantitative polymerase chain reaction (RT-qPCR) testing. However, limited testing capacities, changes in test availability over time, and reporting delays all influence the ability of routine testing to detect underlying changes in infection incidence (3–5). The question of whether changes in case counts at different times reflect epidemic dynamics or simply changes in testing have economic, health, and political ramifications.
RT-qPCR tests provide semiquantitative results in the form of cycle threshold (Ct) values, which are inversely correlated with log10 viral loads, but they are often reported only as binary “positives” or “negatives” (6, 7). It is common when testing for other infectious diseases to use this quantification of sample viral load, for example, to identify individuals with higher clinical severity or transmissibility (8–11). For SARS-CoV-2, Ct values may be useful in clinical determinations about the need for isolation and quarantine (7, 12), identification of the phase of an individual’s infection (13, 14), and predictions of disease severity (14, 15). However, individual-level decision-making on the basis of Ct values has not been widely implemented, owing to measurement variation across testing platforms and samples and a limited understanding of SARS-CoV-2 viral kinetics in asymptomatic and presymptomatic infections. Although a single high Ct value may not guarantee a low viral load in one specimen—for example, because of variable sample collection—measuring high Ct values in many samples will indicate a population with predominantly low viral loads. Cross-sectional distributions of Ct values should therefore represent viral loads in the underlying population over time, which may coincide with changes in the epidemic trajectory. For example, a systematic increase in the distribution of quantified Ct values has been noted alongside epidemic decline (12, 14, 16).
Here, we demonstrate that Ct values from single or successive cross-sectional samples of RT-qPCR data can be used to estimate the epidemic trajectory without requiring additional information from test positivity rates or serial case counts. We demonstrate that population-level changes in the distribution of observed Ct values can arise as an epidemiological phenomenon, with implications for interpreting RT-qPCR data over time in light of emerging SARS-CoV-2 variants. We also demonstrate how multiple cross-sectional samples can be combined to improve estimates of population incidence, a measure that is often elusive without serological surveillance studies. Collectively, we provide metrics for monitoring outbreaks in real time—using Ct data that are collected but currently usually discarded—and our methods motivate the development of testing programs intended for outbreak surveillance.
Relationship between observed Ct values and epidemic dynamics
First, we show that the interaction of within-host viral kinetics and epidemic dynamics can drive changes in the distribution of Ct values over time, without a change in the underlying pathogen kinetics. That is, population-level changes in Ct value distributions can occur without systematic changes in underlying postinfection viral load trajectories at the individual level. To demonstrate the epidemiological link between transmission rate and measured viral loads or Ct values, we first simulated infections arising under a deterministic susceptible-exposed-infectious-recovered (SEIR) model (Fig. 1A and Materials and methods, “Epidemic transmission models”). Parameters used are supplied in table S1. At selected testing days during the outbreak, simulated Ct values are observed from a random cross-sectional sample of the population using the Ct distribution model described in the “Ct value model” section of the Materials and methods and shown in figs. S1 and S2. By drawing simulated samples for testing from the population at specific time points, these simulations recreate realistic cross-sectional distributions of detectable viral loads across the course of an epidemic. Throughout, we assume everyone is infected at most once, ignoring reinfections because these appear to be a negligible portion of infections in the epidemic so far (17).
(A) Per capita daily incidence (histogram) and daily growth rate (blue line) of new infections in a simulated epidemic using an SEIR model. (B) Median days since infection versus daily growth rate of new infections by epidemic day. Labeled points here, and in (E) to (G), show five time points in the simulated epidemic. (C) Observed Ct value by day for 500 randomly sampled infected individuals. (D) Viral kinetics model (increasing Ct value after peak and subsequent plateau near the limit of detection), demonstrating the time course of Ct values (x axis; line shows mean, and ribbon shows 95% quantile range) against days since infection (y axis). Note that the y axis is arranged to align with (E). (E) Distribution of days since infection (violin plots and histograms) for randomly selected individuals over the course of the epidemic. Median and first and third quartiles are shown as green lines and points, respectively. (F) Skewness of observed Ct value distribution versus daily growth rate of new infections by epidemic day. (G) Distribution of observed Ct values (violin plots and histograms) among sampled infected individuals by epidemic day. Median and first and third quartile are shown as purple lines and points, respectively. (H) Time-varying effective reproductive number, Rt, derived from the SEIR simulation, plotted against median and skewness of observed Ct value distribution.
” data-icon-position=”” data-hide-link-title=”0″>

(A) Per capita daily incidence (histogram) and daily growth rate (blue line) of new infections in a simulated epidemic using an SEIR model. (B) Median days since infection versus daily growth rate of new infections by epidemic day. Labeled points here, and in (E) to (G), show five time points in the simulated epidemic. (C) Observed Ct value by day for 500 randomly sampled infected individuals. (D) Viral kinetics model (increasing Ct value after peak and subsequent plateau near the limit of detection), demonstrating the time course of Ct values (x axis; line shows mean, and ribbon shows 95% quantile range) against days since infection (y axis). Note that the y axis is arranged to align with (E). (E) Distribution of days since infection (violin plots and histograms) for randomly selected individuals over the course of the epidemic. Median and first and third quartiles are shown as green lines and points, respectively. (F) Skewness of observed Ct value distribution versus daily growth rate of new infections by epidemic day. (G) Distribution of observed Ct values (violin plots and histograms) among sampled infected individuals by epidemic day. Median and first and third quartile are shown as purple lines and points, respectively. (H) Time-varying effective reproductive number, Rt, derived from the SEIR simulation, plotted against median and skewness of observed Ct value distribution.
Early in the epidemic, infection incidence grows rapidly, and thus most infections arise from recent exposures. As the epidemic wanes, however, the average time elapsed since exposure among infected individuals increases as the rate of new infections decreases (Fig. 1, B and E) (18). This is analogous to the average age being lower in a growing versus declining population (19). Although infections are usually unobserved events, we can rely on an observable quantity, such as viral load, as a proxy for the time since infection. Because Ct values change asymmetrically over time within infected hosts (Fig. 1C), with peak viral load occurring early in the infection, a random sampling of individuals during epidemic growth is more likely to sample recently infected individuals in the early phase of their infection and therefore with higher quantities of viral RNA. Conversely, randomly sampled infected individuals during epidemic decline are more likely to be in the later phase of infection, typically sampling lower quantities of viral RNA, although there is substantial sampling and viral load variability at all time points (Fig. 1D). The overall distribution of observed Ct values under randomized surveillance testing therefore changes over time, as measured by the median, quartiles, and skewness (Fig. 1G). Although estimates for an individual’s time since infection based on a single Ct value will be highly uncertain, the population-level distribution of observed Ct values will vary with the growth rate—and therefore Rt—of new infections (Fig. 1, F and H).
To summarize this key observation in the context of classic results, we find that fast-growing epidemiologic populations (Rt > 1 and growth rate r > 0) will have a predominance of new infections and thus of high viral loads, and shrinking epidemics (Rt < 1 and r < 0) will have more older infections and thus low viral loads at a given cross section, where the relationship between Rt and r is modulated by the distribution of generation intervals (20). Similar principles have been applied to serologic data to infer unobserved individual-level infection events (16, 21–23) and population-level parameters of infectious disease spread (21, 24–28).
We find that this phenomenon might also be present, though less pronounced, among Ct values obtained under symptom-based surveillance, where individuals are identified and tested after symptom onset. Similar to the case of random surveillance testing, Ct values obtained through the testing of recently symptomatic individuals are predicted to be lower (i.e., viral loads are higher) during epidemic growth than those obtained during epidemic decline (figs. S3 and S4). However, defining the exact nature and strength of this relationship will depend on a number of conditions being met (fig. S4, caption).
By modeling the variation in observed Ct values arising from individual-level viral growth and clearance kinetics and sampling errors, the distribution of observed Ct values in a random sample becomes an estimable function of the times since infection, and the expected median and skewness of Ct values at a given point in time are then predictable from the epidemic growth rate. This function can then be used to estimate the epidemic growth rate from a set of observed Ct values. A relationship between Ct values and epidemic growth rate exists under most sampling strategies, as described above, but calibrating the precise mapping is necessary to enable inference (e.g., using a different RT-qPCR; fig. S5). This mapping can be confounded by testing biases arising, for example, from delays between infection and sample collection date when testing capacity is limited or through systematic bias toward samples with higher viral loads, such as those from severely ill individuals. Here, we focus on the case of random surveillance testing, where individuals are sampled at a random point in their infection course.
Inferring the epidemic trajectory using a single cross section
From these relationships, we derive a method to infer the epidemic growth rate given a single cross section of randomly sampled RT-qPCR test results. The method combines two models: (i) the probability distribution of observed Ct values (and the probability of a negative result) conditional on the number of days between infection and sampling and (ii) the likelihood of being infected on a given day before the sample date. For the first, we use a Bayesian model and define priors for the mode and range of Ct values after infection on the basis of the existing literature (Materials and methods, “Ct value model” and “Single cross section model”). For the second, we initially develop two models to describe the probability of infection over time: (i) constant exponential growth of infection incidence and (ii) infections arising under an SEIR model. Both models provide estimates for the epidemic growth rate but make different assumptions regarding the possible shape of the outbreak trajectory: The exponential growth model assumes a constant growth rate over the preceding 5 weeks and requires few prior assumptions, whereas the SEIR model assumes that the growth rate changes daily depending on the remaining number of susceptible individuals but requires more prior information.
To demonstrate the potential of this method with a single cross section from a closed population, we first investigate how the distribution of Ct values and prevalence of PCR positivity changed over time in four well-observed Massachusetts long-term care facilities that underwent SARS-CoV-2 outbreaks in March and April of 2020 (29). In each facility, we have the results of near-universal PCR testing of residents and staff from three time points after the outbreak began, including the number of positive samples, the Ct values of positive samples, and the number of negative samples (Materials and methods, “Long-term care facilities data”). To benchmark our Ct value–based estimates of the epidemic trajectory, we first estimated the trajectory using a standard compartmental modeling approach fit to the measured point prevalences over time in each facility (Fig. 2A). Specifically, we fit a simple extended SEIR (SEEIRR) model, with additional exposed and recovered compartments describing the duration of PCR positivity (Materials and methods, “Epidemic transmission models”), to the three observed point prevalence values from each facility. Because the testing was nearly universal, this approach provides a near ground truth of the epidemic trajectory, against which we can evaluate the accuracy of the Ct value–based approaches. We call this the baseline estimate. Figure 2 shows results and data for one of the long-term care facilities, and figs. S6 and S7 show results for the other three.
(A) Estimated prevalence [faint orange lines show posterior samples, solid orange line shows posterior median, and orange ribbon shows 95% credible intervals (CrIs)] and incidence (red line shows posterior median and red ribbon shows 95% CrI) from the standard compartmental (SEEIRR) model fit to point prevalence at three sampling times (error bars show 95% binomial confidence intervals). (B) Model-predicted Ct distributions (blue) fitted to the observed Ct values (gray bars) from each of three cross-sectional samples. Shown are the posterior median (black line) and 95% CrI for the expected Ct distribution (dark blue ribbon) and 95% prediction intervals based on simulated observations (light blue ribbon). Note that prediction intervals are much wider than CrIs because they result from simulating observations with a small sample size. (C) Each panel shows results from fitting the Ct-based SEIR model separately to three cross sections of virologic data. Shown are random posterior samples (red lines) and the maximum posterior probability (MAP) trajectory (black line) for the incidence curve. (D) Fitted median (blue point) and 95% CrI (blue error bars) for the proportion of samples testing positive based on the Ct model compared with the observed proportion tested positive (gray cross). (E) Thirty-five–day (green) and 1-day (pink) average growth rates from the Ct model estimates in (C) at three time points (violin plots) compared with growth-rate estimates from the SEEIRR model in (A) (lines and shaded ribbons).
” data-icon-position=”” data-hide-link-title=”0″>

(A) Estimated prevalence [faint orange lines show posterior samples, solid orange line shows posterior median, and orange ribbon shows 95% credible intervals (CrIs)] and incidence (red line shows posterior median and red ribbon shows 95% CrI) from the standard compartmental (SEEIRR) model fit to point prevalence at three sampling times (error bars show 95% binomial confidence intervals). (B) Model-predicted Ct distributions (blue) fitted to the observed Ct values (gray bars) from each of three cross-sectional samples. Shown are the posterior median (black line) and 95% CrI for the expected Ct distribution (dark blue ribbon) and 95% prediction intervals based on simulated observations (light blue ribbon). Note that prediction intervals are much wider than CrIs because they result from simulating observations with a small sample size. (C) Each panel shows results from fitting the Ct-based SEIR model separately to three cross sections of virologic data. Shown are random posterior samples (red lines) and the maximum posterior probability (MAP) trajectory (black line) for the incidence curve. (D) Fitted median (blue point) and 95% CrI (blue error bars) for the proportion of samples testing positive based on the Ct model compared with the observed proportion tested positive (gray cross). (E) Thirty-five–day (green) and 1-day (pink) average growth rates from the Ct model estimates in (C) at three time points (violin plots) compared with growth-rate estimates from the SEEIRR model in (A) (lines and shaded ribbons).
As time passes, the distribution of observed Ct values at each time point in the long-term care facilities (Fig. 2B) shifts higher (lower viral loads) and becomes more left skewed. We observed that these shifts tracked with the changing (i.e., declining) prevalence of infection in the facilities. To assess whether these changes in Ct value distributions reflected underlying changes in the epidemic growth rate, we fit the exponential growth and simple SEIR models using the Ct likelihood to each individual cross section of Ct values to get posterior distributions for the epidemic trajectory up to and at that point in time (Fig. 2C). The only facility-specific data for each of these fits were the Ct values and number of negative tests from each single cross-sectional sample. Additional ancillary information included prior distributions for the epidemic seed time (after 1 March) and the within-host virus kinetics. To assess the fit, we compare the predicted Ct distribution (Fig. 2B) and point prevalence (Fig. 2D) from each fit with the data and compare the growth rates from these fits with the baseline estimates. Posterior distributions of all Ct value model parameters are shown in fig. S8.
Although both sets of results are fitted models, and so neither can be considered the truth, we find that the Ct method fit to one cross section of data provides a similar posterior median trajectory to the baseline estimate, which required three separate point prevalences with near-universal testing at each time point. In particular, the Ct-based models appear to accurately discern whether the samples were taken soon or long after peak infection incidence. Both methods were in agreement over the direction of the past average and recent daily growth rates (i.e., whether the epidemic is currently growing or declining and whether the growth rate has dropped relative to the past average). The average growth-rate estimates were very similar between the prevalence-only and Ct value models at most time points, although the daily growth rate appeared to decline earlier in the prevalence-only compartmental model. These estimates have a great deal of variability, however, and should be interpreted in that context. This is especially clear in fig. S7, where the other facilities exhibit more variability between estimates from the two methods. Overall, these results show that a single cross section of Ct values can provide similar information to point-prevalence estimates from three distinct sampling rounds when the epidemic trajectory is constrained, as in a closed population.
To ensure that our method provides accurate estimates of the full epidemic curve, we performed extensive simulation-recovery experiments using a synthetic closed population undergoing a stochastic SEIR epidemic. Figure S9 shows the results of one such simulation, demonstrating the information gained from using a single cross section of virological test data when attempting to estimate the true infection incidence curve at different points during an outbreak. We assessed performance using simulated data from populations of different sizes and varied key assumptions of the inference method. Specifically, we implemented a version of the method that uses only positive Ct values without information on the fraction positive and tested the impact using prior distributions of decreasing strengths. Details are provided in the “simulated long-term care facility outbreaks” section of the supplementary materials, and results are in figs. S10 to S12.
Although no real long-term care facility data were available to assess the method’s accuracy during the early phase of the epidemic outbreak, the simulation experiments reveal that the method can be used at all stages of an epidemic. Furthermore, although there is a substantial uncertainty in the growth-rate estimates, these analyses show that a single cross section of data can be used to determine whether the epidemic has been recently increasing or decreasing. The posterior probability of growth versus decline can be used for this assessment, acting like a hypothesis test when the credible interval excludes zero or in a broader inferential way if it does not. Although this is a trivial result for SARS-CoV-2 incidence in many settings, where cases, hospitalizations, or deaths already provide a clear picture of epidemic growth or decline, for locations and future outbreaks where testing capacity is restricted, our results show that a single cross-sectional random sample of a few hundred tested individuals combined with reasonable priors (for example, constraining the epidemic seed time to within a 1- to 2-month window) could be used to immediately estimate the stage of an outbreak. Moreover, this inferential method provides the basis for combining cross sections for multiple testing days.




